The answer should be easy. Or not? There are several options: The one that best fits to reality, The one that requires less training data, The one that is not overfitted, etc. Actually, it is maybe as simple as selecting the one that you like most, the one that you are able to calibrate, your customers preferred one…
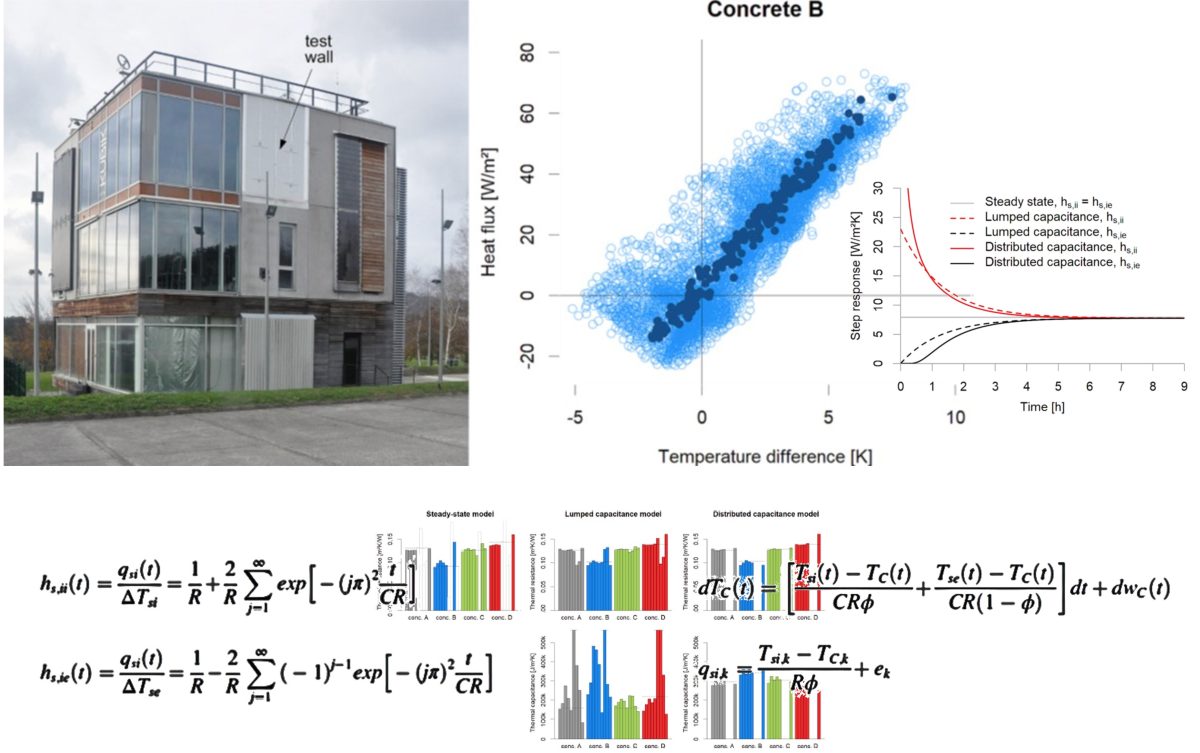
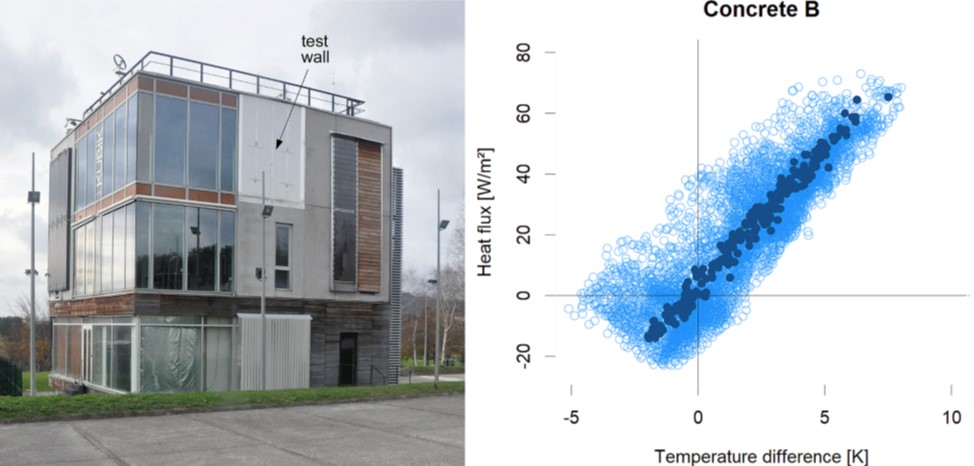
My colleague Beñat Arregi worked for some time over some concrete walls within project ECOBINDER. These were tested in KUBIK some years ago. By itself, the heat transfer of walls is quite simple, with linear relations associated to indoor-outdoor temperature differences. But there are very relevant dynamics involved, associated with thermal storage, the impact of solar radiation, and variations in boundary conditions.
And he tried several modelling approaches. So, the question came to us. Which is the best model to use? We could have developed our own criteria, but maybe it was already answered by our previous generations. It seems that Urban Norlen already had a thought on this almost 30 years ago.
There was a generation of researchers working on experimental heat transfer assessment around the Passys & Paslink initiatives 30 to 40 years ago, which developed their procedures with much more limited technology than what we have today. Some of these made a fantastic work on passing their knowledge through Dynastee, and IEA annexes 58 & 71.
Coming back to the models… Norlen defined a few key criteria on model development that should be considered always (maybe longer in the original source):
- Simplicity: Smaller models are preferable, limiting the number of parameters insofar as reasonable.
- Identifiability: Models should allow the determination of their parameters uniquely from the data.
- Fit to the data: Models should be able to explain most of the variance in the data.
- Internal validity: The model should remain reliable when exposed to new conditions (test data) different than those used for parameter estimation (training data).
- External validity: Results obtained with the models should not conflict with previous knowledge or experience without a well justified explanation.
- Dynamic stability: For dynamic models, transients effect induced by temporary variations in input variables should fade out over time.
So, we took these criteria and applied it to three type of models:
- A steady-state model. Basically, a U-value calculation though averaging processes.
- A lumped capacitance model. Formulated as a linear stochastic differential equation (SDE) in continuous time
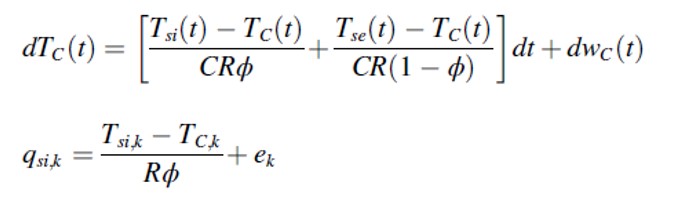
- A distributed capacitance model. Considering that the walls were homogeneous, there was an analytical solution available, which was modeled through its step response function.
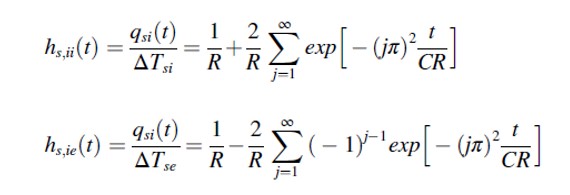
All of these are quite common approaches in literature, but they were never compared in a structured way. So here are the findings:
- Simplicity. If we are only interested in U-value calculation, and the climate is sufficiently severe (i.e., indoor-outdoor temperature differences greater than 10ºC), then steady-state methods are suitable. If there is a need to consider thermal storage in the walls, it’s a different story.
- Identifiability. Identifying thermal resistance can be performed using one month of data or so. Provided that this data is from winter months. If thermal capacity is relevant, the distributed capacity model delivered consistent outcomes quite independently of the period.
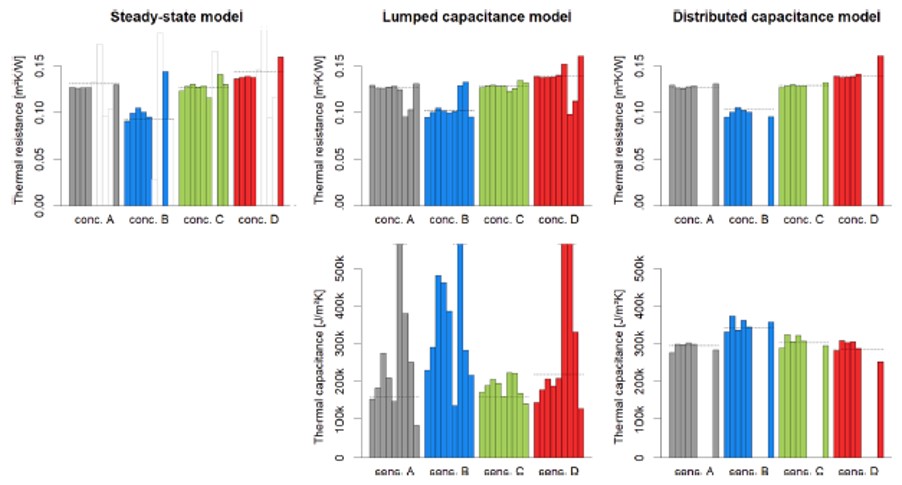
- Fit to the data. When trying to fit hourly values, steady-state models are not suitable (obviously). Both lumped and distributed capacitance models worked fine in winter months but did not provide accurate values with lower indoor-outdoor temperature differences (even with thermal inversion) and greater solar radiation in summer.
- Internal validity. We did short-term predictions here. Unsurprisingly, steady-state models were not useful here. The other two models predicted well under stable indoor conditions and large indoor-outdoor temperature differences, but the distributed capacitance model was found to be more successful for periods with lower temperature differences and greater variations in internal conditions.
- External validity. Here, the thermal capacitance was checked. Again, the distributed capacitance model provided better estimates. This is, estimates closer to those reported in scientific literature.
- Dynamic stability. All three models seem to be dynamically stable, without relevant deviations on the longer timespan (>5h). The distributed capacitance model seems to provide smoother responses to inputs.
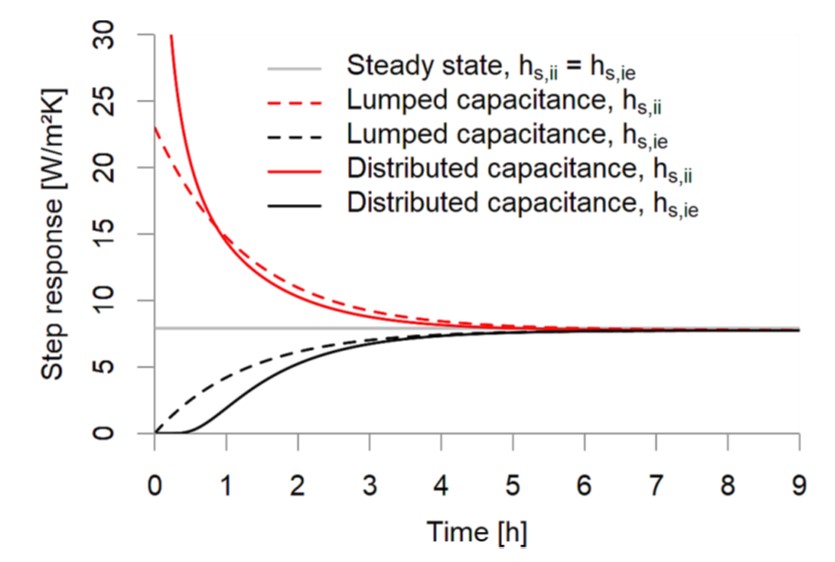
As a general conclusion, I believe that distributed capacitance models seem to be very useful here. But that using them is only possible if the modeled system is homogeneous. This issue may potentially be overcome if analytical solutions for more complex wall systems are found and tested. But there are still many open questions to answer.
For day-to-day U-value assessments, the steady-state method in the standard keeps being a great tool (if its sufficiently cold outside).
It was a pleasure to get in this journey with Beñat Arregi and Juan Carlos Ramos. I hope that we have been able to get some useful outcomes for the scientific community. The reference to the full paper is available below.
I would also like to add that there are fantastic scientific works out there. But that it is increasingly difficult to access many of these. Papers from workshops and conferences are only available in the bookshelves of a few researchers across the world. As times goes by, they will retire, and someone will throw away these. They do not have a DOI and do not exist in the digital world. In our case, I would like to give credit to Maria Jose Jimenez, who provided a scanned copy of the work by Norlen. In a broader sense, this showcases the relevance of repositories in the scientific community. Otherwise, whatever you achieve, it will be lost in a few decades.
Maybe, the paragraph above proves that I’m already starting to get older.
Reference to our work:
Beñat Arregi, Roberto Garay-Martinez, Juan Carlos Ramos, Estimation of thermal resistance and capacitance of a concrete wall from in situ measurements: A comparison of steady-state and dynamic models, Energy and Buildings, Volume 296, 2023, 113393, ISSN 0378-7788, https://doi.org/10.1016/j.enbuild.2023.113393
Reference to the original work by Urban Norlen:
U. Norlen, Determining the thermal resistance from in-situ measurements, in: Work. Appl. Syst. Identif. Energy Savings Build., 1994: pp. 402–429.